2021.05.08 - [Tech.log/자료구조] - [자료구조의 형태]
[자료구조의 형태]
자료구조란 ? 컴퓨터에서 사용할 자료를 더 효율 적으로 관리하기 위해서 자료의 특성과 사용 용도에 따라 분류하고 구조화 한것이다. 1. 단순 자료 구조 컴퓨터 프로그래밍에서 쓰이는 데이터
itfordoit.tistory.com
트리란
그래프의 일부이지만 사이클이 없는 계층적 구조이다. 트리에는 여러가지 종류가 있는데 살펴보자.
이진트리
각각의 노드가 최대 두 개의 자식 노드를 가지는트리 자료구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.
정 이진 트리(Full Binary Tree)
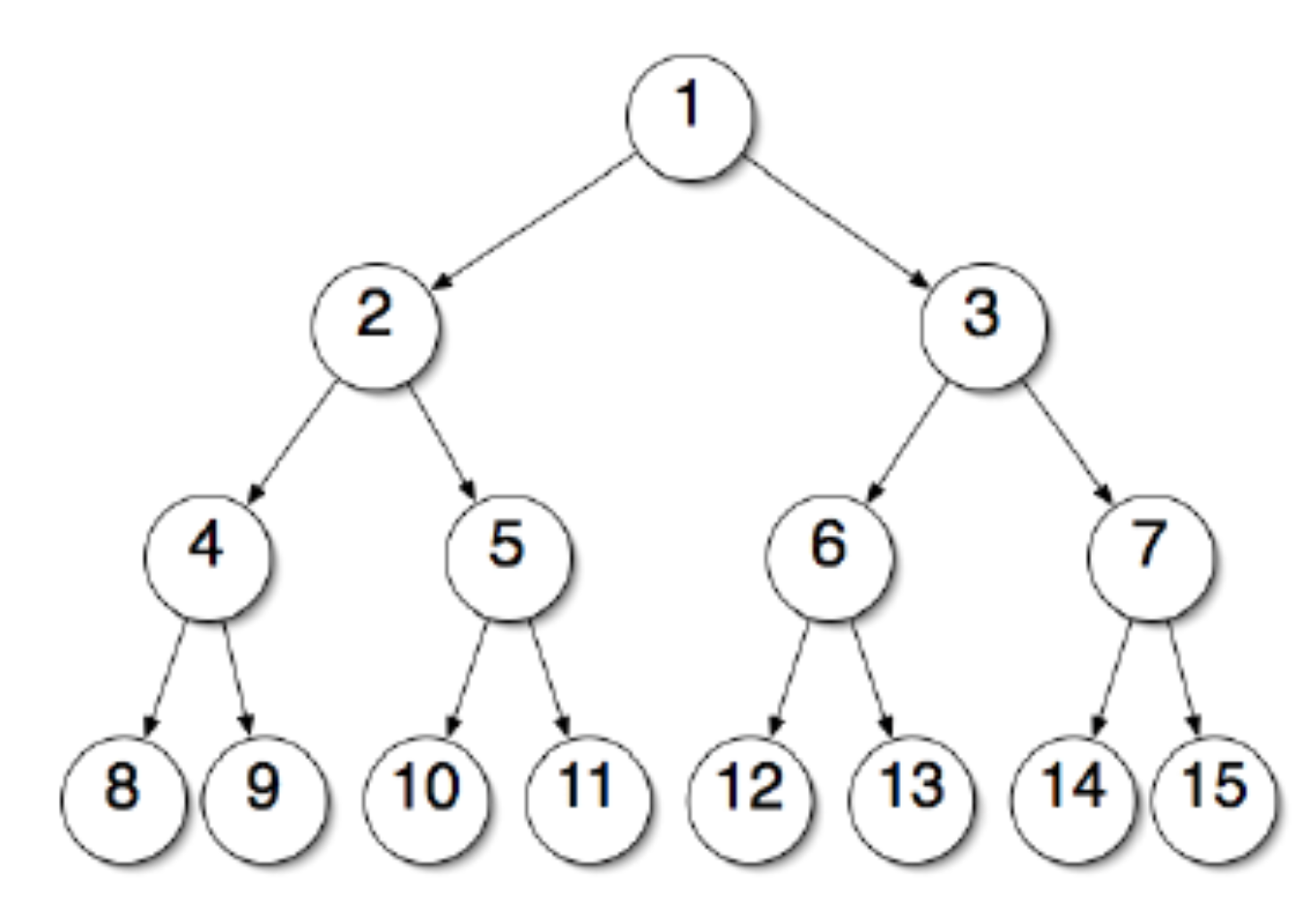
모든 레벨에서 노드들이 꽉 채워진 자식노드 2개를 가지고 있는 이진트리다.
완전 이진트리(Complete Binary Tree)

"이진 트리"중 노드가 왼쪽부터 차례대로 채워져 있는 트리를 말한다.
이진 탐색 트리(Binary Search Tree)

이진탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조
이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안됐습니다.
이진 탐색은 탐색의 소요되는 시간 복잡도는 O(logn)이지만, 자료의 입력과 삭제가 어렵다.
연결 리스트의 경우 자료 삽입,삭제의 시간복잡도는 O(1)이지만, 탐색이 O(n)이다.
이 둘을 합친 것이 이진 탐색 트리이다.
이진탐색트리의 특징
각 노드의 왼쪽 서브 트리에는 해당 노드 보다 작은 값으로 이루어져 있다.
각 노드의 오른쪽 서브 트리에는 해당 노드보다 큰 값으로 이루어져있다.
중복된 노드가 없다.
이진탐색트리의 탐색
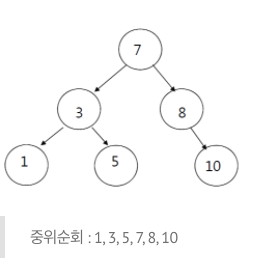
이진탐색트리를 순회할 때는 중위순회(inorder) 방식을 사용한다.(왼=>현재노드=>오른쪽 )
이진탐색트리의 연산
탐색
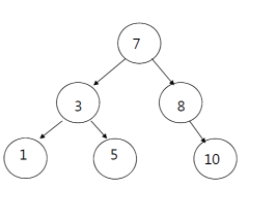
만일 10을 탐색한다고 했을때,
1. 7와 10 비교 =>오른쪽
2.8과 10비교 =>오른쪽
3.종료
따라서 탐색 시에 소요되는 최대 복잡성은 트리의 높이인 h O(h)가 된다.
파이썬 코드
def find(self, val):
if (self.findNode(self.root, val) is False):
return False
else:
return True
def findNode(self, currentNode, val):
if (currentNode is None):
return False
elif (val == currentNode.val):
return currentNode
elif (val < currentNode.val):
return self.findNode(currentNode.leftChild, val)
else:
return self.findNode(currentNode.rightChild, val)
삽입
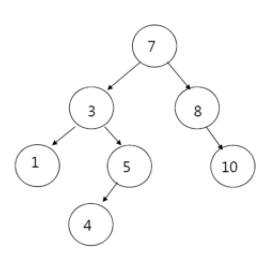
4를 추가한다.
1. 7와 4비교 =>왼
2.3과 4비교 =>오른쪽
3.4와5비교 =>왼쪽
4. 추가
따라서 삽입 시에 소요되는 최대 복잡성은 트리의 높이(h)인 O(h)가 된다.
def insert(self, val):
if (self.root is None):
self.setRoot(val)
else:
self.insertNode(self.root, val)
def insertNode(self, currentNode, val):
if (val <= currentNode.val):
if (currentNode.leftChild):
self.insertNode(currentNode.leftChild, val)
else:
currentNode.leftChild = Node(val)
elif (val > currentNode.val):
if (currentNode.rightChild):
self.insertNode(currentNode.rightChild, val)
else:
currentNode.rightChild = Node(val)
삭제
삭제는 여러가지 상황이 있다. 하나 씩 따져보자.
- 자식노드가 없는 경우
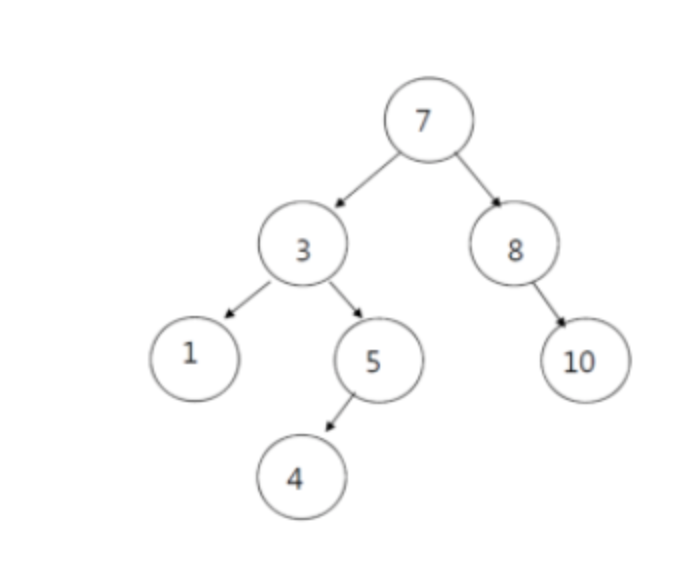

4를 제거하려는 경우
그냥 없애면 된다
.
- 자식 노드가 하나 있는 경우

20을 지우고 싶은 경우
해당 노드를 지우고 자식 노드와 연결하면 된다.
- 자식 노드가 두개 있는 경우
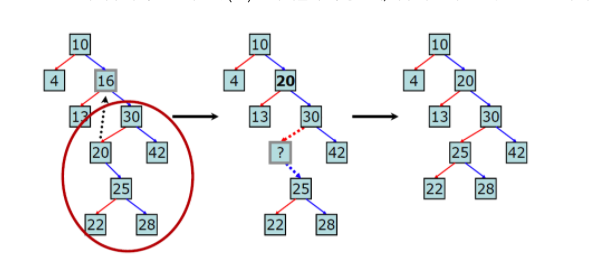
16을 지우고 싶은 경우
16의 왼쪽 서브트리에 속한 모든 값은 16보다 작고, 오른쪽 서브트리에 속한 모든 값은 16보다 큰 것을 확인할 수 있습니다.
특히 13을 predecessor(삭제 대상 노드의 왼쪽 서브트리 가운데 최대값), 20을 successor(삭제 대상 노드의 오른쪽 서브트리 가운데 최소값)라고 한다.
따라서 아래와 같이 삭제할 노드인 16 위치에 20을 복사해 놓고, 기존 20 위치에 있던 노드를 삭제하게 되면 정렬된 순서를 유지(=이진탐색트리 속성을 만족)할수있다.
- 삭제 대상 노드의 오른쪽 서브트리를 찾는다.
- successor(1에서 찾은 서브트리의 최소값) 노드를 찾는다.
- 2에서 찾은 successor의 값을 삭제 대상 노드에 복사한다.
- successor 노드를 삭제한다.
트리의 높이가 ℎh이고 삭제대상 노드의 레벨이 𝑑라고 가정했을때 , 1번 과정에서는 𝑑번의 비교 연산이 필요합니다. 2번 successor 노드를 찾기 위해서는 삭제 대상 노드의 서브트리 높이(ℎ−𝑑h−d)에 해당하는 비교 연산을 수행. 3번 4번은 복사하고 삭제하는 과정으로 상수시간이 걸려 무시할 만 합니다. 종합적으로 따지면 𝑂(𝑑+ℎ−𝑑)O(d+h−d), 즉 𝑂(ℎ)O(h)가 됩니다.삭제 시에 소요되는 최대 복잡성은 트리의 높이(h)인 O(h)가 된다.
//이진트리의 중위 순회 파이썬 코드
def traverse(self):
return self.traverseNode(self.root)
def traverseNode(self, currentNode):
result = []
if (currentNode.leftChild is not None):
result.extend(self.traverseNode(currentNode.leftChild))
if (currentNode is not None):
result.extend([currentNode.val])
if (currentNode.rightChild is not None):
result.extend(self.traverseNode(currentNode.rightChild))
return result
한계점

만일 극단적인 상황일 경우, 높이만 높고 노드의 수는 적은 상황이 발생한다. 이런 상황에서는 탐색 속도가 O(n)으로 ) O(logn)이라고 하기 어렵다. 이를 위해 트리의 균형을 맞추는 AVL Tree가 생겼다.
AVL Tree
이진 탐색트리를 보완한 균형 트리이다.BF는 왼쪽과 오른쪽 서브트리의 높이 차 이다.
식으로는 다음과 같이 BF = hL - hR로 쓰며,이 값이 -1, 0, 1일 때만 균형있는 트리라고 본다.
만일 -1,0,1이 아닐 경우 불균형 트리라고 보고 회전을 사용하여 맞춘다.

초기 상태

15삽입

3 삽입
이때, 높이의 차이가 2이기 때문에 회전한다.
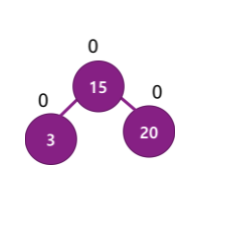
짜잔!

12삽입

5 삽입후 불균형이 생긴다. 불균형은 삽입 한 노드로 부터 올라가는 식으로 먼저 해결 해야한다.

3,5,12의 중간 숫자를 가운데로 배치 해준다.

11삽입
마찬가지로 불균형이 생긴다.
따라서 불균형이 생긴 기점을 시작으로 12,5,15의 가운데인 12를 기준으로 회전한다.

이때 11과 20이 남는다. BST의 삽입과 똑같은 방식으로 진행하면 된다.

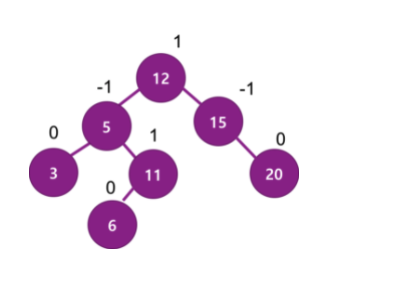
6삽입

40삽입
불균형이 생긴다. 해소해주자.

Red-Black Tree
'Tech.log > 자료구조' 카테고리의 다른 글
| [자료구조의 심화] (0) | 2021.05.10 |
|---|---|
| [자료구조의 형태] (0) | 2021.05.08 |
| [Java] Java Collections Framework 알아보기 (0) | 2021.04.15 |




댓글